study research

CUDA Basic

Intro

在CUDA中，host和device是两个重要的概念，我们用host指代CPU及其内存，而用device指代GPU及其内存。CUDA程序中既包含host程序，又包含device程序，它们分别在CPU和GPU上运行。一个CUDA程序的执行流程如下：

  1. 分配host内存，并进行数据初始化；
  2. 分配device内存，并从host将数据拷贝到device上；
  3. 调用CUDA的核函数在device上完成指定的运算；
  4. 将device上的运算结果拷贝到host上；
  5. 释放device和host上分配的内存。

核函数（kernel）是CUDA中的一个重要概念，它是在device上线程中并行执行的函数。核函数用__global__符号声明，在调用时需要用<<<grid, block>>>来指定kernel要执行的线程数量，在CUDA中，每一个线程都要执行核函数，并且每个线程会分配一个唯一的线程号thread ID，这个ID值可以通过核函数的内置变量threadIdx来获得。

CUDA中有3个函数限定词：

  • __global__：在device上执行，从host中调用，异步，返回类型必须是void，不支持可变参数参数，不能成为类成员函数。
  • __device__：在device上执行，但仅可以从device中调用，不可以和__global__同时用。
  • __host__：在host上执行，仅可以从host上调用。默认限定词。

例如考虑以下程序：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

#include <stdio.h>

__global__ void hello_world(void)
{
    printf("GPU: Hello world!\n");
}

int main(int argc, char **argv)
{
    printf("CPU: Hello world!\n");
    hello_world<<<1, 10>>>();
    cudaDeviceReset(); // if no this line ,it can not output hello world from gpu
    return 0;
}

kernel在执行被定义的线程数量是10，所以GPU上的hello world会被打印10次。注意到核函数的执行是异步的，这时我们加一句cudaDeviceReset()，以确保程序在核函数执行完毕之后才退出主线程。

image-20230306105248040

CUDA 线程管理

GPU上很多并行化的轻量级线程，核函数在device上执行时实际上是启动很多线程，一个kernel所启动的所有线程称为一个网格（grid），同一个网格上的线程共享相同的全局内存空间，grid是线程结构的第一层次，而网格又可以分为很多线程块（block），一个线程块里面包含很多线程。

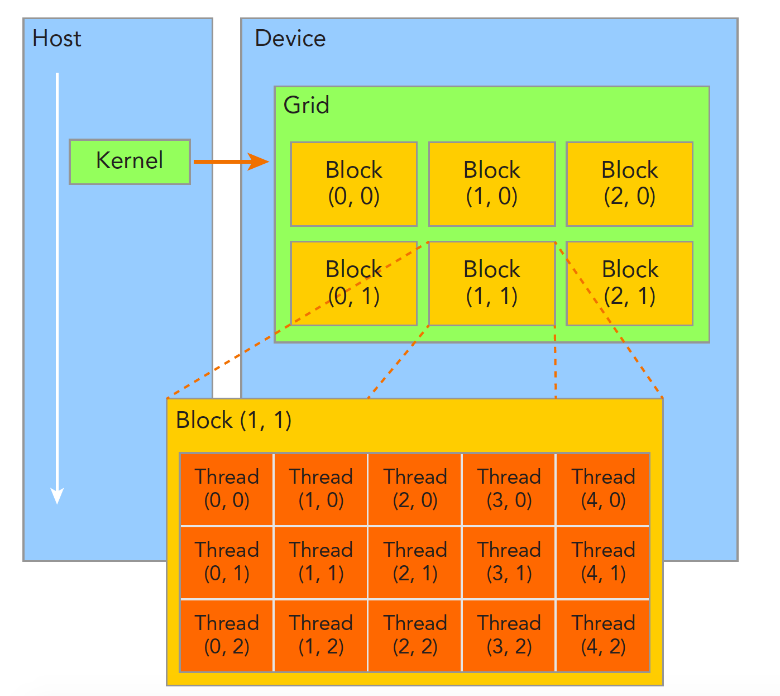
image-20230306105746085

之后是线程的标号。grid和block都是定义为dim3类型的变量，dim3可以看成是包含三个无符号整数（x，y，z）成员的结构体变量，在定义时，缺省值初始化为1。因此grid和block可以灵活地定义为1-dim，2-dim以及3-dim结构（上图所示是一个2-dim的grid-block结构）。代码如下所示：

1
2
3

dim3 grid(3, 2);
dim3 block(5, 3);
kernel_fun<<< grid, block >>>(prams...);

每一个核函数都有两个内置的坐标变量blockIdx，threadIdx，标识其在(grid, block)中的位置。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <cuda_runtime.h>
#include <stdio.h>

__global__ void checkIndex(void)
{
    printf("threadIdx:(%d,%d,%d) blockIdx:(%d,%d,%d) blockDim:(%d,%d,%d) gridDim:(%d,%d,%d)\n",
           threadIdx.x, threadIdx.y, threadIdx.z,
           blockIdx.x, blockIdx.y, blockIdx.z, blockDim.x, blockDim.y, blockDim.z,
           gridDim.x, gridDim.y, gridDim.z);
}

int main(int argc, char **argv)
{
    int nElem = 6;
    dim3 block(3);
    dim3 grid((nElem + block.x - 1) / block.x);
    printf("grid.x %d grid.y %d grid.z %d\n", grid.x, grid.y, grid.z);
    printf("block.x %d block.y %d block.z %d\n", block.x, block.y, block.z);
    checkIndex<<<grid, block>>>();
    cudaDeviceReset();
    return 0;
}

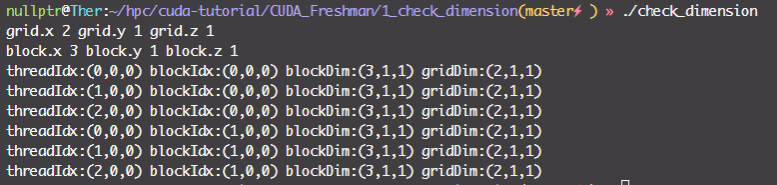
image-20230306110845229

此处注意，一个block上的线程是放在同一个流式多处理器（SM）上的。但是单个SM的资源有限，这导致线程块中的线程数是有限制的（1024）。CUDA采用单指令多线程（SIMT）架构来管理和执行线程，每32个线程为一组，被称为线程束（Warp），线程束中所有线程同时执行相同的指令。我们可以用以下代码获取GPU的一些硬件信息：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

#include <iostream>

int main(int argc, char **argv)
{
    int dev = 0;
    cudaDeviceProp devProp;
    cudaGetDeviceProperties(&devProp, dev);
    std::cout << "GPU device " << dev << ": " << devProp.name << std::endl;
    std::cout << "SM number: " << devProp.multiProcessorCount << std::endl;
    std::cout << "shared memory per block: " << devProp.sharedMemPerBlock / 1024.0 << " KB" << std::endl;
    std::cout << "max threads per block: " << devProp.maxThreadsPerBlock << std::endl;
    std::cout << "max threads per multiprocessor: " << devProp.maxThreadsPerMultiProcessor << std::endl;
}

image-20230306112643191

实战1——矩阵加法

CUDA多线程并行的能力，经常用来将串行代码中的for并行化。例如，如果我们需要计算两个向量的和，串行写法如下：

1
2
3
4

void sumArraysOnHost(float *A, float *B, float *C, const int N) {
  for (int i = 0; i < N; i++)
    C[i] = A[i] + B[i];
}

而在并行写法下，我们只需要开若干个线程同步执行：

1
2
3
4

__global__ void sumArraysOnGPU(float *A, float *B, float *C) {
  int i = threadIdx.x;
  C[i] = A[i] + B[i];
}

接下来，我们使用CUDA编程的方法实现一个基础运算——矩阵乘法。我们的两个矩阵大小是4096x4096，由于一个线程块中的线程数上限是1024(32x32)，所以我们需要的grid数是128x128。定义方法如下：

1
2
3
4
5

int nx = 1 << 12;
int ny = 1 << 12;
int nBytes = nx * ny * sizeof(float);
dim3 block(32, 32);
dim3 grid((nx - 1) / block.x + 1, (ny - 1) / block.y + 1);

调用方法如下：

1

sumMatrix<<<grid, block>>>(A_dev, B_dev, C_dev, nx, ny);

之后我们看在CPU上进行串行计算的代码。在此处我们利用指针将二维矩阵展开为一维矩阵进行处理：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

void sumMatrix2DonCPU(float *MatA, float *MatB, float *MatC, int nx, int ny)
{
    float *a = MatA;
    float *b = MatB;
    float *c = MatC;
    for (int j = 0; j < ny; j++)
    {
        for (int i = 0; i < nx; i++)
        {
            c[i] = a[i] + b[i];
        }
        c += nx;
        b += nx;
        a += nx;
    }
}

而编写GPU核函数的关键是定位线程执行的布局。例如对于函数kernel_name<<<4,8>>>(argument list)，其线程布局为：

image-20230306120517383

据此可以得到每一个线程的唯一标识符，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

__global__ void sumMatrix(float *MatA, float *MatB, float *MatC, int nx, int ny)
{
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    int iy = threadIdx.y + blockDim.y * blockIdx.y;
    int idx = ix + iy * ny;
    if (ix < nx && iy < ny)
    {
        MatC[idx] = MatA[idx] + MatB[idx];
    }
}

完整代码见CUDA编程入门（三）从矩阵加法例程上手CUDA编程。

实战2——矩阵乘法

使用一维向量实现二维矩阵乘法，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

void cpu_mat_mul(int *mat1, int *mat2, int *result)
{
    for (int r = 0; r < R_SIZE; r++)
    {
        for (int c = 0; c < R_SIZE; c++)
        {
            for (int n = 0; n < R_SIZE; n++)
            {
                result[r * R_SIZE + c] += mat1[r * R_SIZE + n] * mat2[n * R_SIZE + c];
            }
        }
    }
}

如果将最外层并行化，可以写作：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

__global__ void gpu_mat_mul(int *mat1, int *mat2, int *result)
{
    const int r = blockIdx.x * THREAD_NUM + threadIdx.x;
    for (int c = 0; c < R_SIZE; c++)
    {
        for (int n = 0; n < R_SIZE; n++)
        {
            result[r * R_SIZE + c] += mat1[r * R_SIZE + n] * mat2[n * R_SIZE + c];
        }
    }
}

当然，此处还有更多的优化空间，有时间再补。

实战3——规约

并行规约指的是，有N个输入数据，使用一个符合结合律的二元操作符作用其上，最终生成1个结果。规约的一般思路如下：首先把输入数组划分为更小的数据块，之后用一个线程计算一个数据块的规约值，最后把所有部分和再求和得出最终结果。

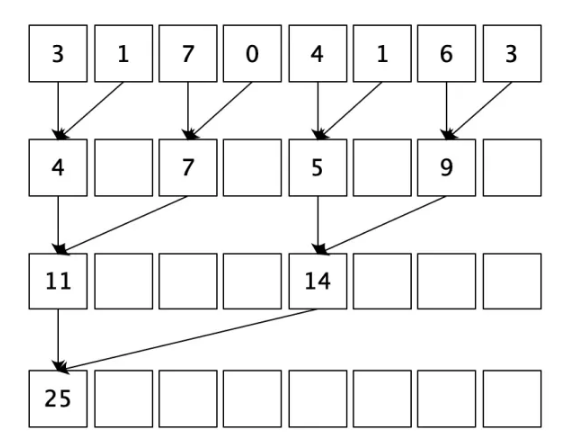
image-20230306142756225

这样，相比于串行实现：

1
2
3

int sum = 0;
for (int i = 0; i < N; i++)
    sum += array[i]

其复杂度为$O(N)$，并行实现的复杂度变为了$O(N\log_2N)$。

我们编写一个递归的CPU程序（注意大部分GPU架构不支持递归）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

int recursiveReduce(int *data, int const size)
{
    // terminate check
    if (size == 1)
        return data[0];
    // renew the stride
    int const stride = size / 2;
    if (size % 2 == 1)
    {
        for (int i = 0; i < stride; i++)
        {
            data[i] += data[i + stride];
        }
        data[0] += data[size - 1];
    }
    else
    {
        for (int i = 0; i < stride; i++)
        {
            data[i] += data[i + stride];
        }
    }
    // call
    return recursiveReduce(data, stride);
}

GPU并行程序如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

__global__ void reduceNeighbored(int * g_idata,int * g_odata,unsigned int n) 
{
    // set thread ID
    unsigned int tid = threadIdx.x;
    // boundary check
    if (tid >= n) return;
    // convert global data pointer
    int *idata = g_idata + blockIdx.x * blockDim.x;
    // in-place reduction in global memory
    for (int stride = 1; stride < blockDim.x; stride *= 2)
    {
        if ((tid % (2 * stride)) == 0)
        {
            idata[tid] += idata[tid + stride];
        }
        // synchronize within block
        __syncthreads();
    }
    // write result for this block to global mem
    if (tid == 0)
    {
        g_odata[blockIdx.x] = idata[0];
    }
}

当然，其实这种算法有一个明显的缺点：只有一半的线程是活跃的，而且每进行一轮计算后，活跃的线程数都会减少一半，这是条件表达式的使用造成的。比如在第一轮迭代时，只有偶数ID的线程会为True，其主体才能得到执行。这会导致线程束的分化，也就是说只有一部分线程是活跃的，但是所有的线程仍然都会被调度。后续的优化将会解决这个问题。

Reference

HPC c++
Licensed under CC BY-NC-SA 4.0
© 2022 - 2023 Ther's Blog
Built with Hugo
Theme Stack designed by Jimmy
visitors: total visits: time(s) reads: time(s)