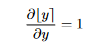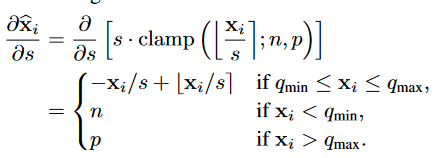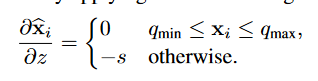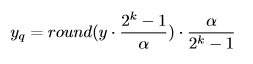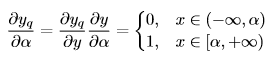study research

QAT串讲和代码实现

本文将对QAT的一些基本算法做一些介绍，然后介绍两种较为直观也较为常用的QAT算法

QAT

首先写出原始形式的量化式： $$ s \cdot {\rm clamp}(\lfloor \frac{x}{s} \rceil;n,p) $$ 或： $$ s \cdot [{\rm clamp}(\lfloor \frac{x}{s} \rceil + \lfloor z \rceil;n,p) - \lfloor z \rceil] $$ STE（直通估计器）最早在Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation1中提出。由于round运算的梯度为0或未定义，STE将舍入算子的梯度近似为1：

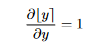
所以舍入值（权重和激活）相对于原值的导数可以定义为：

LSQ

本文主要提出了两种方法：

  1. 提供了一种简单的方法来近似量化器步长的梯度，它对量化的状态转换很敏感，可以说在学习步长作为一个模型参数时提供了更精细的优化。
  2. 提出了一个简单的启发式方法，使步长更新的幅度与权重更新达到更好的平衡，以改善收敛性。

LSQ2这一工作引入了可学习的步长$s$:

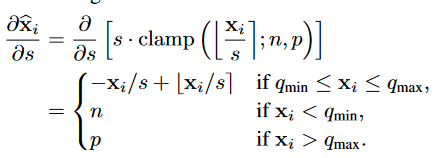
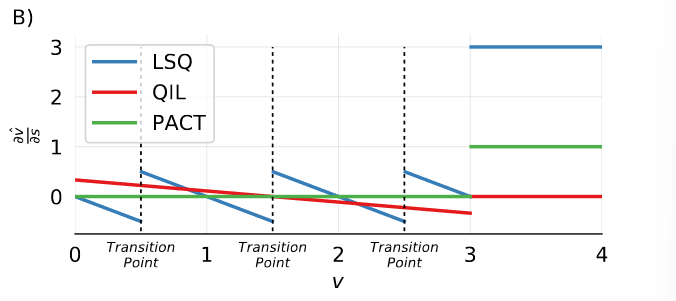
LSQ的巧妙之处在于，它模拟了量化过程中的一个现象：一个给定的$x_i$离量化过渡点越近，它就越有可能由于对$s$的更新改变其量化值$\hat x_i$，导致$\hat x_i$出现大幅度跳跃——梯度随着$x_i$到过渡点的距离减少而增加。

在更新之前，激活和权重的初始步长值为： $$ s_{init} = \frac{2\bar x}{\sqrt{p}} $$ 在训练过程中，我们期望步长参数随着精度的提高而变小（因为数据被更精细地量化），而步长更新随着量化项目的增加而变大（因为在计算其梯度时，更多的项目被加在一起）。对此我们需要将总损失与一个调节参数相乘：$g=1/\sqrt{n p}$（$n$为每一层权重/激活的参数量）。同时将所有矩阵乘法层的输入激活和权重设置为2位、3位、4位或8位，但第一层和最后一层始终使用8位。

LSQ+

LSQ方法大多基于以ReLU为激活函数的模型。但对于GeLU这样的函数，正负范围分布不均，无论是使用无符号量化范围量化（将所有负值钳制为0）还是使用有符号量化范围量化（对激活函数的负和正部分给予同等重视）都会造成精度损失。

LSQ+3这一工作引入了可学习的偏置$z$:

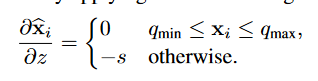
这样，我们就可以在激活处执行非对称量化，提高精度。

对于权重，我们使用对称量化： $$ s_{init} = \max(|\mu - 3\sigma|,|\mu + 3\sigma|) / 2^{b-1} $$ 对于激活，我们通过校准最小化下式： $$ s_{init}, \beta_{init} = \arg \min_{s,\beta} ||\hat x - x||_F^2 $$

PACT

本文解决了量化中的一个核心问题：如何在range和precision之间寻找到tradeoff。特别是对于激活来说，这一问题尤其严重。绝大多数activation集中在某个很小的范围，但总有一些outlier点 会离中心非常远。这些outlier的value比较大，如果删除的话，会造成较大的误差。但是，如果你用outlier的最大值来作为range来量化整个数据，又面临着precision不够的问题。

传统的激活函数没有任何可训练的参数，因此量化激活产生的误差无法用BP算法补偿。而传统的ReLU函数输出值域是无界的，这造成了更大的动态范围误差。

PACT函数的定义如下：

$$ y = PACT(x) = 0.5 (|x| - |x-\alpha| + \alpha) $$

随后是其量化过程：

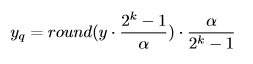
image-20221117141630233

更新$\alpha$的梯度表达式如下（注意到计算第一次倒数时使用了一个直通估计器）：

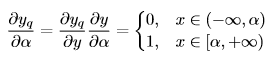
image-20221117143805146

注意到此处的scaling factor并非通过传统方法得到，因此量化表达式有较大的差异。重新改写上式：

$$ s \cdot {\rm clamp}(\lfloor \frac{x}{s} \rceil;0,\alpha), s = \frac{\alpha}{2^k -1} $$

Code

首先给出PyTorch中自定义求导算子的写法官方文档：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Exp(Function):
    @staticmethod
    def forward(ctx, i):
        result = i.exp()
        ctx.save_for_backward(result)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        result, = ctx.saved_tensors
        return grad_output * result

# Use it by calling the apply method:
output = Exp.apply(input)

借助此，我们可以自定义函数的正向传播和反向传播过程。以下代码参考自45。

STE

首先我们给出BNN中STE（效果如下图所示）的表达式：

1
2
3
4
5
6
7
8

class STEFunction(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input):
        return (input > 0).float()

    @staticmethod
    def backward(ctx, grad_output):
        return F.hardtanh(grad_output)

在真正作为一个module使用时，需要进行封装：

1
2
3
4
5
6
7

class StraightThroughEstimator(nn.Module):
    def __init__(self):
        super(StraightThroughEstimator, self).__init__()

    def forward(self, x):
        x = STEFunction.apply(x)
        return x

对于一般的round函数，其STE可以做如下构造：

1
2
3
4
5
6
7
8

class STE(torch.autograd.Function):
    @staticmethod
    def forward(ctx, x):
        return torch.round(x)

    @staticmethod
    def backward(ctx, grad_output):
        return grad_output.clone()

我们可以看下这种写法和直接使用torch.round()函数的区别：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# original
print('version 1')
x = torch.tensor([0., 100., 200.], requires_grad = True)
out = x.round()
loss = out.mean()
loss.backward()
print(x.grad)

# modified
print('version 2')
x = torch.tensor([0., 100., 200.], requires_grad = True)
out = STE.apply(x)
loss = out.mean()
loss.backward()
print(x.grad)

1
2
3
4

version 1
tensor([0., 0., 0.])
version 2
tensor([0.3333, 0.3333, 0.3333])

可以看到，原生的round函数不产生任何梯度。

此外，还有一种更精妙的写法：

1
2
3
4

def round_pass(x):
    y = x.round()
    y_grad = x
    return y.detach() - y_grad.detach() + y_grad

此函数的意味是：函数的返回值为y - y_grad + y_grad = x.round()，但反向传播的梯度仍然按照y_grad = x的梯度去算。

按照此种写法还可以实现“梯度倍增”的效果：

1
2
3
4

def grad_scale(x, scale):
    y = x
    y_grad = x * scale
    return y.detach() - y_grad.detach() + y_grad

LSQ

LSQ的正向传播和反向传播在STE的基础上实现，同时还有初始化规则：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class LsqQuan(Quantizer):
    def __init__(self, bit, all_positive=False, symmetric=False, per_channel=True):
        super().__init__(bit)

        if all_positive:
            assert not symmetric, "Positive quantization cannot be symmetric"
            # unsigned activation is quantized to [0, 2^b-1]
            self.thd_neg = 0
            self.thd_pos = 2 ** bit - 1
        else:
            if symmetric:
                # signed weight/activation is quantized to [-2^(b-1)+1, 2^(b-1)-1]
                self.thd_neg = - 2 ** (bit - 1) + 1
                self.thd_pos = 2 ** (bit - 1) - 1
            else:
                # signed weight/activation is quantized to [-2^(b-1), 2^(b-1)-1]
                self.thd_neg = - 2 ** (bit - 1)
                self.thd_pos = 2 ** (bit - 1) - 1

        self.per_channel = per_channel
        self.s = torch.nn.Parameter(torch.ones(1))

    def init_from(self, x, *args, **kwargs):
        if self.per_channel:
            self.s = torch.nn.Parameter(
                x.detach().abs().mean(dim=list(range(1, x.dim())), keepdim=True) * 2 / (self.thd_pos ** 0.5))
        else:
            self.s = torch.nn.Parameter(x.detach().abs().mean() * 2 / (self.thd_pos ** 0.5))

    def forward(self, x):
        if self.per_channel:
            s_grad_scale = 1.0 / ((self.thd_pos * x.numel()) ** 0.5)
        else:
            s_grad_scale = 1.0 / ((self.thd_pos * x.numel()) ** 0.5)
        s_scale = grad_scale(self.s, s_grad_scale)

        x = x / s_scale
        x = torch.clamp(x, self.thd_neg, self.thd_pos)
        x = round_pass(x)
        x = x * s_scale
        return

LSQ+同理，只不过在原有基础上引入偏移量z，并使用不同的初始化规则，此处不再详细说明。

PACT

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class LearnedClippedLinearQuantization(nn.Module):
    def __init__(self, num_bits, init_act_clip_val, dequantize=True, inplace=False):
        super(LearnedClippedLinearQuantization, self).__init__()
        self.num_bits = num_bits
        self.clip_val = nn.Parameter(torch.Tensor([init_act_clip_val]))
        self.dequantize = dequantize
        self.inplace = inplace

    def forward(self, input):
        # Clip between 0 to the learned clip_val
        input = F.relu(input, self.inplace)
        # Using the 'where' operation as follows gives us the correct gradient with respect to clip_val
        input = torch.where(input < self.clip_val, input, self.clip_val)
        with torch.no_grad():
            scale, zero_point = asymmetric_linear_quantization_params(self.num_bits, 0, self.clip_val, signed=False)
        input = LinearQuantizeSTE.apply(input, scale, zero_point, self.dequantize, self.inplace)
        return input

    def __repr__(self):
        inplace_str = ', inplace' if self.inplace else ''
        return '{0}(num_bits={1}, clip_val={2}{3})'.format(self.__class__.__name__, self.num_bits, self.clip_val.item(),
                                                           inplace_str)

Reference

  1. http://arxiv.org/abs/1308.3432 ↩︎

  2. http://arxiv.org/abs/2004.09576 ↩︎

  3. http://arxiv.org/abs/2110.01900 ↩︎

  4. https://zhuanlan.zhihu.com/p/72681647 ↩︎

  5. https://github.com/zhutmost/lsq-net ↩︎

© 2022 - 2023 Ther's Blog
Built with Hugo
Theme Stack designed by Jimmy
visitors: total visits: time(s) reads: time(s)