AMP 混合精度训练
混合精度(Mix Precision)训练是指在训练时,对网络不同的部分采用不同的数值精度,对追求速度的算子(比如 conv、matmul)可以用较低精度(比如 float16)从而获得明显的性能提升,而对其它更看重精度的算子(比如 log、softmax)则保留较高的精度(比如 float32)。另外,模型在内存中用FP16做储存和乘法从而加速计算,而用FP32做累加避免舍入误差。混合精度训练的策略有效地缓解了舍入误差的问题。

此外,在计算时,其梯度值可能会超出FP16的范围,在这种情况下,将对梯度值进行缩放,使其落在FP16范围内。
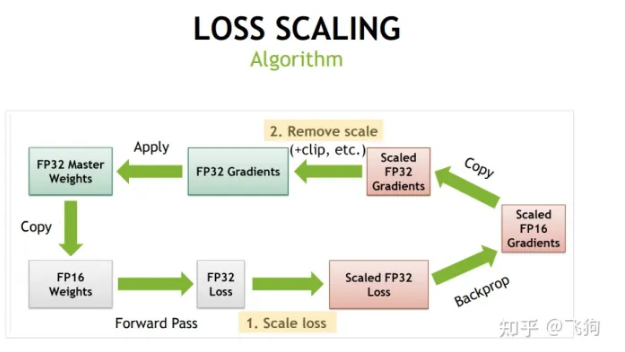
此外还引入损失放大机制,通过放大loss的值来防止梯度的underflow(只在BP时传递梯度信息使用,真正更新权重时还是要把放大的梯度再unscale回去)。
BF16
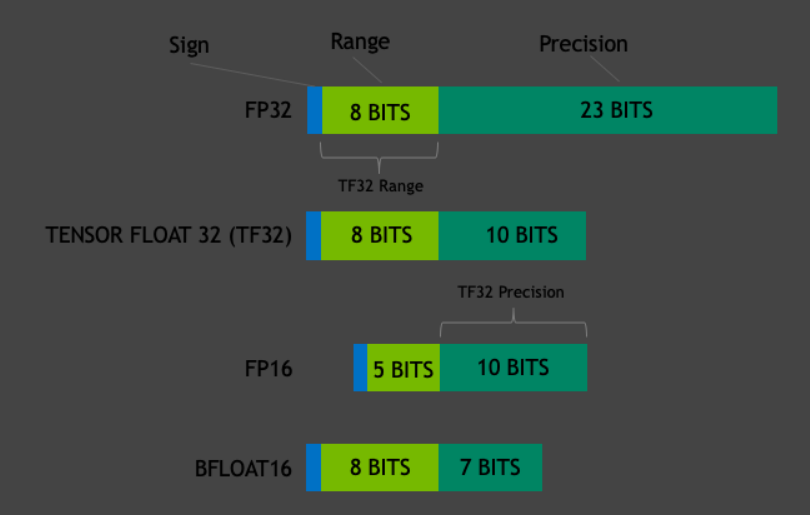
BF16由google提出,它在范围上与FP32相同,但精度上有所差异(可以看做FP32的直接截断版,因此与FP32之间的转换要比FP16方便):

支持BF16的框架有:
- Google TPUs and Tensorflow.
- Nvidia CUDA TensorCore
- Intel Intel Habana Gaudi, Xeon processors (AVX-512 BF16 extensions), and Intel FPGAs
- Arm ArmV8.6-A
- AMD AMD ROCm
TF32
TF32(注意只有19bit)在设置上相当于BF16(范围)和FP16(精度)的混合体。
HFP8
如果直接使用FP8(1-4-3)进行推理,会发现精度的明显降低;而如果用FP8(1-4-3)进行训练会导致更差的后果(因为权值、激活和梯度的数据范围相差很大)。HFP8在forward时使用FP-1-4-3,backward时使用FP-1-5-2。
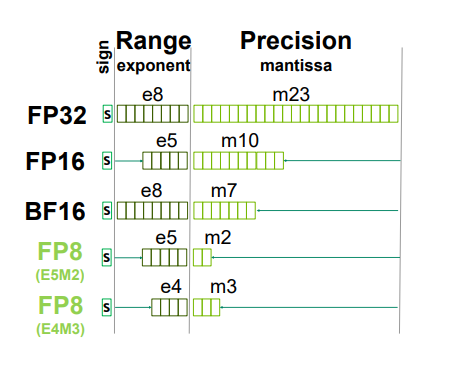
我们对其进行更加细致的数值分析,假设指数位为$e$,尾数位为$m$,其公式如下: $$ f = (-1)^s 2^{p-b}(1+\frac{d_1}{2}+\cdots + \frac{d_m}{2^m}), b=2^{e-1}(\rm adjustable) $$ 直观的讲,对于一个区间$[2^a,2^{a+1}],a\in Z$来说,间隔长度为$2^{a-m}$。注意这种设置方法在绝对值小时有着较为密集的分布,这对于大多呈正态分布的权重、激活分布有一定的好处。
这里我们重点介绍下HFP8在Transformer中的应用。NVIDIA的H100支持两种格式的FP8:比如 FP8(1-4-3) 多用于来表示 weights 和 activation,而 FP8(1-5-2) 来表示gradients。其基本架构如下图所示,注意累加后的值仍然为FP32/FP16:
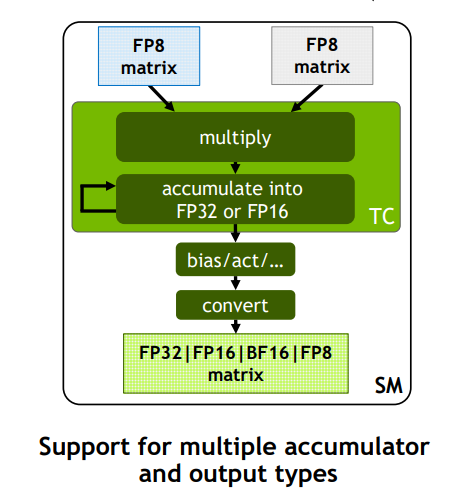
相比于bit数相同的int8,FP8有以下优点:
- FP8的电路可以和FP16/32的电路进行重用。
- int8和FP32的转换需要进行quantize和dequantize,造成额外的开销;而FP8和FP32只需要直接舍掉指数和尾数的精度,不需要进行quantize和dequantize(当然,需要确定合适的指数尾数划分)。