Dataflow

乘加累计单元

机器学习中的核心计算单元被称为乘積累加单元（Multiply Accumulate, MAC）。它使用一条指令进行以下运算： $$ a \leftarrow a + b \times c $$

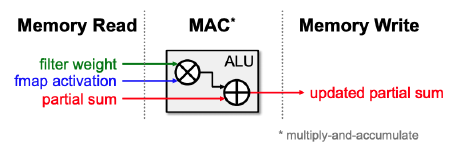
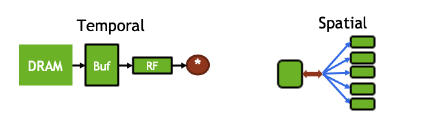
为减小其数据搬移所造成的的开销，我们需要关注其数据的重复使用，对此我们采取以下方法：

• Temporal reuse：单个数据被同一个计算单元重复使用多次
• Spatial reuse：单个数据被多个不同的计算单元同时使用

OS Dataflow & WS Dataflow

基于这样的思想，我们可以设计两种不同的dataflow（以下的代码以1D conv为例）：

• Output Stationary Dataflow：输出的同一数据在时间上相邻，便于输出数据的重用

1
2
3
4
5
6
7

for (q=0; q<Q; q++) // 输出的循环位于外层
{
    for (s=0; s<S; s++)
    {
        OA[q] += IA[q+s] * W[s];
    }
}

这一重用可以在output侧加入寄存器实现：

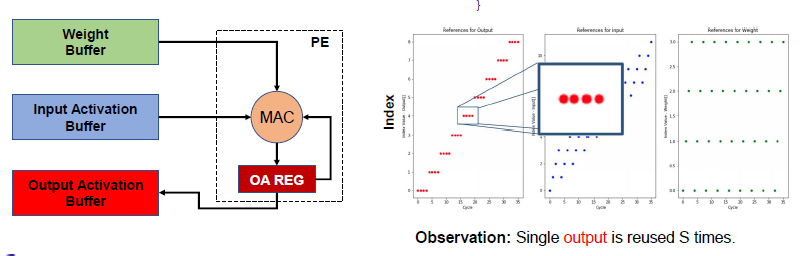
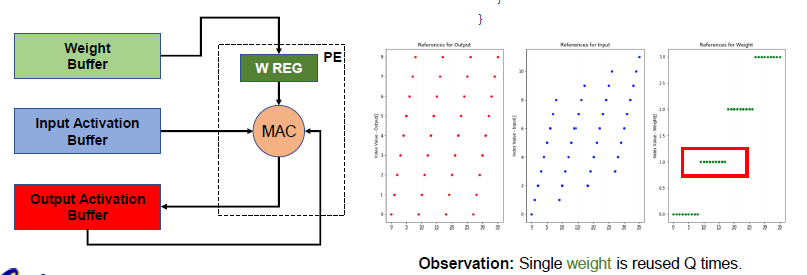
• Weight Stationary Dataflow：权重的同一数据在时间上相邻，便于权重数据的重用

1
2
3
4
5
6
7

for (s=0; s<S; s++) // 权重的循环位于外层
{
    for (q=0; q<Q; q++)
    {
        OA[q] += IA[q+s] * W[s];
    }
}

这一重用可以在weight侧加入寄存器实现：

Accelerator

接下来，我们将在乘加单元的基础上探索更加宏观层面的矩阵乘法的高效数据流计算。

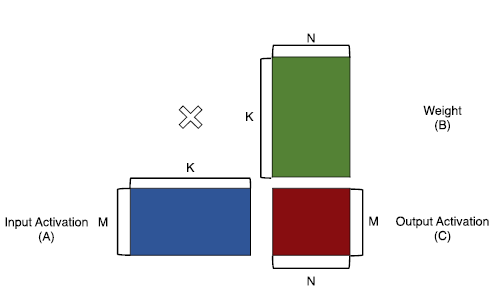
首先我们写出一般矩阵乘法的计算流：

1
2
3
4
5
6
7
8

for (m=0; m<M; m++) {
    for (n=0; n<N; n++) {
        OA[n,m] = 0;
        for (k=0; k<K; k++) {
            OA[n,m] += IA[m, k] * W[k, n];
        }
    }
}

数据的并行化大致可以分为两种方法：Spatial-K和Spatial-N。

Spatial-K旨在将IA中一行和W中一列的计算并行化：

1
2
3
4
5
6
7
8

for (m=0; m<M; m++) {
    for (n=0; n<N; n++) {
        OA[n,m] = 0;
        spatial_for (k=0; k<K; k++) {
            OA[n,m] += IA[m, k] * W[k, n];
        }
    }
}

Spatial-N旨在将W中的一行进行广播：

1
2
3
4
5
6
7
8

for (m=0; m<M; m++) {
    spatial_for (n=0; n<N; n++) {
        OA[n,m] = 0;
        for (k=0; k<K; k++) {
            OA[n,m] += IA[m, k] * W[k, n];
        }
    }
}

当然，我们也可以将其进行组合：

1
2
3
4
5
6
7
8

for (m=0; m<M; m++) {
    spatial_for (n=0; n<N; n++) {
        OA[n,m] = 0;
        spatial_for (k=0; k<K; k++) {
            OA[n,m] += IA[m, k] * W[k, n];
        }
    }
}

Adder Tree

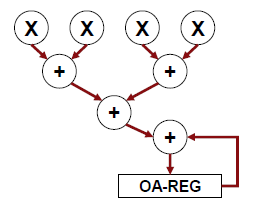
加法树（Adder Tree）采用了一种以空间换取时间的策略。为了同时计算多个IA[m, k] * W[k, n]，可以将多个加法器堆叠组成树状结构：

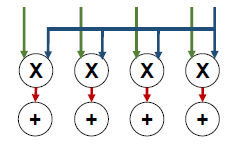
Direct-Wiring Multicast

将权重的一行进行广播，使得权重的N列可以同时计算：

Systolic Array

脉动阵列（Systolic Array）既可以实现Spatial-K中的加速（Systolic Accleration）功能，也可以实现Spatial-N中的广播（Systoic Multicast）功能。这里我们直接将两者组合以说明其功能。

考虑一个基本的矩阵乘法$C=AB$，weight stationary的systolic array计算方式如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// stage 1
c_11 = a_11 * b_11
// stage 2
c_11 += a_12 * b_21
c_12 = a_11 * b_12
c_21 = a_21 * b_11
// stage 3
c_12 += a_12 * b_22
c_21 += a_22 * b_21
c_22 = a_21 * b_12
// stage 4
c_22 += a_22 * b_22

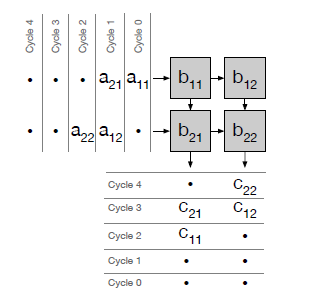
如果考虑到$B$的预装，计算方式改为：

1
2
3
4
5
6
7
8

// stage 1
move B and do not load
// stage 2
load b_11, b_21
// stage 3
load b_12, b_22
c_11 = a_11 * b_11
// stage 4 and after same as systolic-1

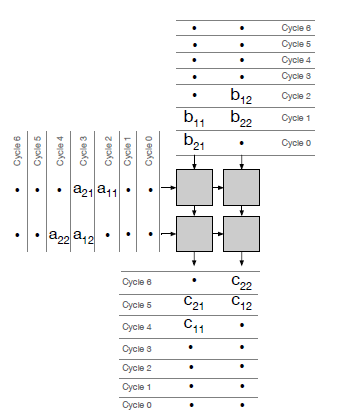
这会带来一个问题：在预装B的时候，我们不能做任何有用的工作。所以，每一个处理单元必须要有至少两个寄存器来存储它负责的B上的元素。在任何特定的周期中，一个寄存器将用于执行乘法累加操作，而另一个寄存器将作为预加载过程的一部分向下传播B的元素。

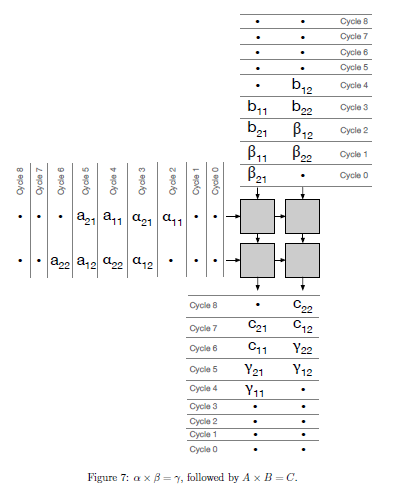
这仍然遗留了一个问题：如果我们想保留之前预装的矩阵，而不是用一个新的矩阵来覆盖它，怎么办？我们如何将其传达给收缩阵列的处理单元？对此可以引入一个1 bit的信号量。

如果传播信号为0，那么第1个寄存器（寄存器0）应该用于向下传播权重，而第2个寄存器（寄存器1）应该用于乘法累加。同样，如果传播信号为1，那么第1个寄存器（寄存器0）应该被用来进行乘法累加，而第2个寄存器（寄存器1）应该被用来向下传播权重。

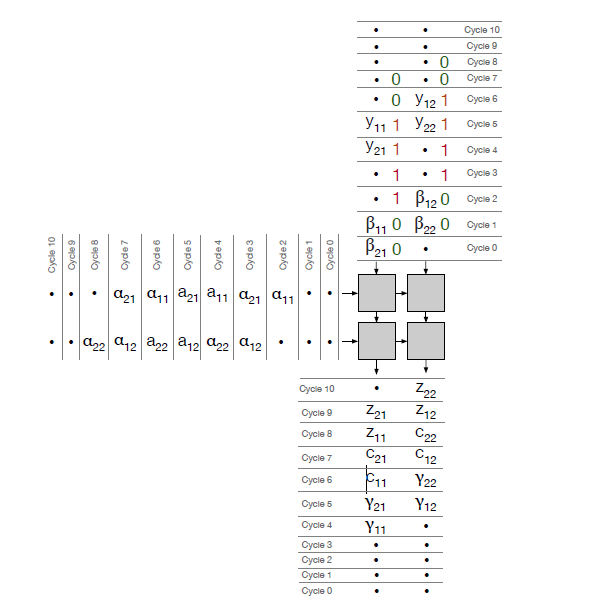
以下是$\alpha \times \beta = \gamma$和$A \times B = C$的例子：由于$\beta$的标识均为0，所以$\beta$由寄存器0向下传播；当$\beta$准备用于计算时，$b$被载入，由于传输信号为1，$b$由寄存器1向下传播，而寄存器0用于乘法的计算。

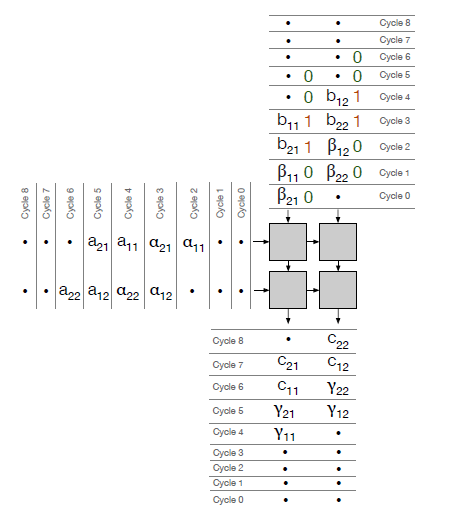
同理有$\alpha \times \beta = \gamma$，$A \times \beta = C$, $\alpha \times Y = Z$的数据流。