本节用到的公式虽然基础，但想要真正理清楚公式之间的关系还是比较麻烦的（博主就被绕晕过）。新人首秀，多多指教~

assignment

本实验是UC Berkeley EECS 本科课程Hardware for Machine Learning的第1个lab。本lab要求将一个简单的LeNet以不同的方式进行量化，并在CIFAR 10数据集上进行测评。具体要求见本文档。

关于量化(quantization)的基本公式本文不再赘述，详见¹。本文主要关注量化的代码实现细节。

method

流程

本文主要介绍静态训练后量化（static post training quantization）。其流程如下：

1. 在浮点环境下训练模型。
2. 使用少量的校正数据，确定激活（activation，即经过中间层的数据流）的数据分布，并得到其scaling factor和zero point（本文简单起见，在量化时不使用zero point，scaling factor使用最常规的公式得到：$S = \frac{r_{\max}-r_{\min}}{q_{\max}-q_{\min}}$），用于后续的推理²。
3. 量化权重（weight）、偏置（bias，可选）和激活，进行全整数推理。

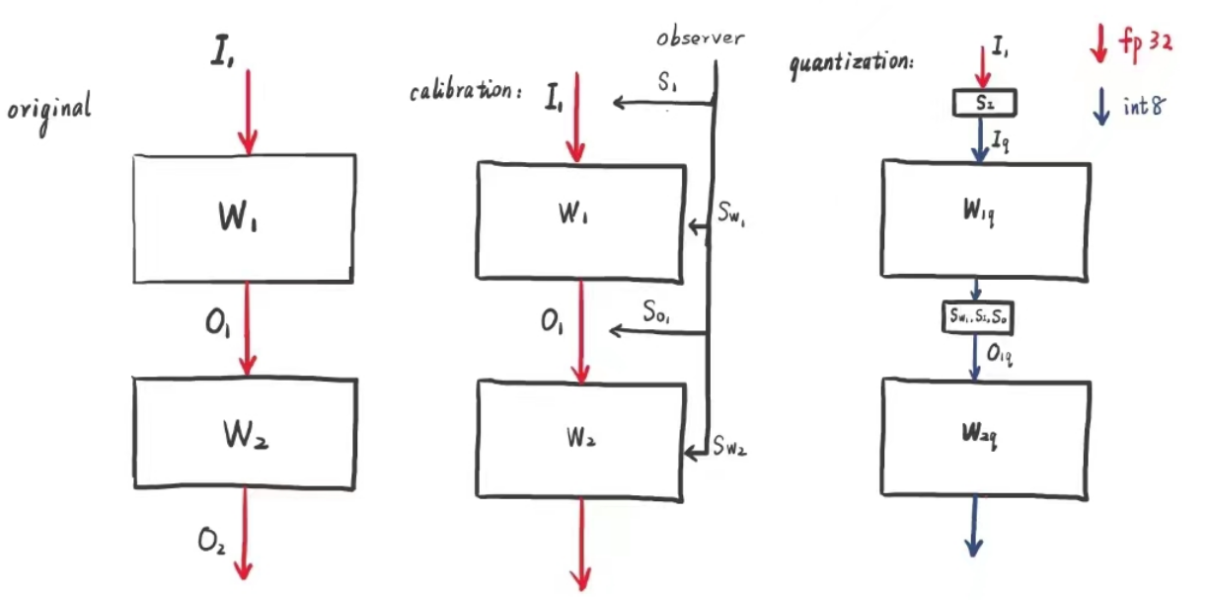
关于weight和activation的量化

假设一个神经网络由$W_1, W_2, W_3\cdots$若干层组成（此处我们假设它们均为线性层，但其他如卷积层等同理）。

$$ O_1 = IW_1 $$

$$ W_{1q} = {\rm clamp}({\rm round}(\frac{W_1}{S_{W_1}}), \min,\max) $$

$$ I_{q} = {\rm clamp}({\rm round}(\frac{I}{S_I}), \min,\max) $$

我们可以得到使用$W_q$和$S_q$重建的$W_r$，$I_r$同理： $$ W_{1r} = S_{W_1}W_{1q} \approx W_1 $$

$$ I_r = S_II_q \approx I $$

则： $$ O_1 \approx W_{1r}I_r \approx S_{W_1}S_IW_{1q}I_q $$

为方便起见，我们在代码中将$W_{1q}I_q$记做$R_1$，将$W_{2q}O_{1q}$记作$R_2$，以此类推。

注意到此处$W_{1r}$和$I_r$均为整数，$S_{W_1}$和$S_I$均为浮点数，则$O$也为浮点数。但当$O$进入下一个计算模块时，同样需要进行整数量化：

$$ O_{1q} = {\rm clamp}({\rm round}(\frac{O_1}{S_{O_1}}), \min,\max) \approx \frac{S_{W_1}S_I}{S_{O_1}}W_{1q}I_q $$

$$ O_{1r} = S_{O_1}O_{1q} \approx O_1 $$

而此处的$\frac{S_{W_1}S_I}{S_{O_1}}$同样可以化为整数的形式，即$\frac{S_{W_1}S_I}{S_{O_1}}\approx2^{-n}$，从而实现真正意义的全整数推理。

对于第二层参数，我们同样有： $$ O_{2} \approx W_{2r}O_{1r} \approx S_{W_2}S_{O_1}W_{2q}O_{1q} $$

$$ O_{2q} = {\rm clamp}({\rm round}(\frac{O_2}{S_{O_2}}), \min,\max) \approx \frac{S_{W_2}S_{O_1}}{S_{O_2}}W_{2q}O_{1q} $$

当计算到最后一层第$n$层时，我们无需获取$S_{O_n}$（因为计算它的唯一目的在于进行后一层的整数推理），于是我们有：

$$ O_{n} \approx O_{nr} = O_{nq}S_{O_n} = S_{W_n}S_{O_{n-1}}W_{nq}O_{(n-1)q} $$

实际上，此处是否获取$S_{O_n}$无关紧要。例如，若此处进行的是图像分类任务，我们需要求出的实际上只是数量之间的比例关系，而不是数量本身。

综上，我们可以得出每一层的scaling factor $S_i$：

• 输入：$S_I$
• 中间层：$\frac{S_{O_1}}{S_{W_1}S_{I}}, \frac{S_{O_2}}{S_{W_2}S_{O_1}}, \cdots, \frac{S_{O_n}}{S_{W_n}S_{O_{n-1}}}$

令$\frac{S_{O_i}}{S_{W_i}S_{O_{i-1}}}=S_i$（当i=0时，$S_{O_{i-1}}$化为$S_I$），则也可以使用递归的方法写作：

$$ S_i = \begin{cases} \frac{S_{O_1}}{S_{W_1}S_I}, i = 1 \ \frac{S_{O_i}}{S_{W_i}S_I\prod_1^{i-1}(S_kS_{W_k})}, i > 1 \end{cases} $$

关于bias的量化

在量化中处理bias有两种较为简单的办法：

1. 使用无bias的模型。
2. 不对bias进行quantization，而是直接使用浮点域的bias和反量化之后的weight、activation乘积进行相加。相加完毕之后再对结果进行量化。

但同样地，我们也可以在整数域进行带bias的推理。我们以本题的场景为例（只对最后一层进行量化），最后一层在浮点域的推理可以表示为：

$$ O_n = W_nO_{n-1} + b_n $$

量化之后的表示为： $$ O_n \approx S_{W_n}S_{O_{n-1}}(W_{nq}O_{(n-1)q} + b_n) $$

据此可以直接得出$b_n$的量化因子为：

$$ S_{b_n} = S_{W_n}S_{O_{n-1}} = S_{W_n}S_I\prod_{k=1}^{n-1}(S_kS_{W_k}) $$

code

本节只呈现一些关键代码

point 1: 量化权重

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from typing import Tuple

def quantized_weights(weights: torch.Tensor, bit: int=8, actual=True) -> Tuple[torch.Tensor, float]:
    if actual:
        maxval = torch.max(weights)
        minval = torch.min(weights)
    else:
        mu = torch.mean(weights)
        sigma = torch.std(weights)
        maxval = mu + 3 * sigma
        minval = mu - 3 * sigma

    maxval = torch.max(-minval, maxval)
    scale = maxval / (2 ** (bit - 1))
    result = torch.round(weights / scale)
    return torch.clamp(result, min=-2**(bit-1), max=2**(bit-1)-1), scale

本节作者在确定数据范围时尝试了两种方法：min/max法和3-sigma法。由于LeNet的权重分布基本类似于正态分布，所以两种策略差距不是很大。

point2: 量化激活

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

    def quantize_activations(activations: np.ndarray, n_w: float, n_initial_input: float, ns: List[Tuple[float, float]], bits = 8) -> float:

        maxval = np.max(activations)
        minval = np.min(activations)
        n_a = (maxval - minval) / (2 ** bits)

        if len(ns) == 0:
            scale = n_a / (n_initial_input * n_w)
        else:
            div = 1
            for n in ns:
                div *= n[0] * n[1]
            scale = n_a / (n_initial_input * n_w * div)
        
        return scale

此处的n_w指代$S_{W_i}$，n_a指代$S_{O_i}$，对于第$i(i\ge2)$层，ns列表中存储的若干对元素为$[S_{W_1},S_1], \cdots, [S_{W_{i-1}},S_{i-1}]$，套用前文关于$S_i$的公式即得。

point3: 正向传播

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

    def forward(self, x: torch.Tensor, bits: int = 8) -> torch.Tensor:
        # You can access the output activation scales like this:
        input_scale = self.input_scale
        fc1_output_scale = self.fc1.output_scale
        fc2_output_scale = self.fc2.output_scale
        fc3_output_scale = self.fc3.output_scale
        conv1_output_scale = self.conv1.output_scale
        conv2_output_scale = self.conv2.output_scale

        I = x
        I_q = torch.clamp(torch.round(I / input_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        R_1 = self.pool(F.relu(self.conv1(I_q)))
        O_1q = torch.clamp(torch.round(R_1 / conv1_output_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        R_2 = self.pool(F.relu(self.conv2(O_1q)))
        O_2q = torch.clamp(torch.round(R_2 / conv2_output_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        O_2q = O_2q.view(-1, 16 * 5 * 5)
        R_3 = F.relu(self.fc1(O_2q))
        O_3q = torch.clamp(torch.round(R_3 / fc1_output_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        R_4 = F.relu(self.fc2(O_3q))
        O_4q = torch.clamp(torch.round(R_4 / fc2_output_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        R_5 = self.fc3(O_4q)
        O_5q = torch.clamp(torch.round(R_5 / fc3_output_scale), min=-2**(bits-1), max=2**(bits-1)-1)
        return O_5q.to(device)

注意clamp操作和round操作插入的位置。

point4: 量化偏置

1
2
3
4
5

def quantized_bias(bias: torch.Tensor, n_w: float, n_initial_input: float, ns: List[Tuple[float, float]], bits: int=32) -> torch.Tensor:
    scale = n_w * n_initial_input
    for n in ns:
        scale *= n[0] * n[1]
    return torch.clamp((bias / scale).round(), min=MIN_32B_SINT, max=MAX_32B_SINT)

同point 2的处理方法。

result

将一些基本结果列入下表：

这里值得一提的是关于偏置的结论：当一个模型有偏置时，如果只量化权重和激活而无视偏置，将会有较大的精度下降，这是因为量化之后整型的权重和激活之积和浮点型的偏置所在的值域有较大的差异。而对最后一层的偏置进行量化后，两者的值域之间的差异大大减少，偏置真正起到了其作用，最后模型输出的误差有所减小，因而精度有所恢复。

不过在实际程序中大多采用“不对bias进行quantization，而是直接使用浮点域的bias和反量化之后的weight、activation乘积进行相加，相加完毕之后再对结果进行量化”的方法。考虑到偏置相加的计算开销要远远小于权重相乘，这样的简便做法是可以被接受的。

reference