method
GAN分为两个基本部分:discriminator和generator。discriminator的输入为train data和fake data(distribution),输出为data True/False的概率分布;generator的输入为random noise,输出为fake data。
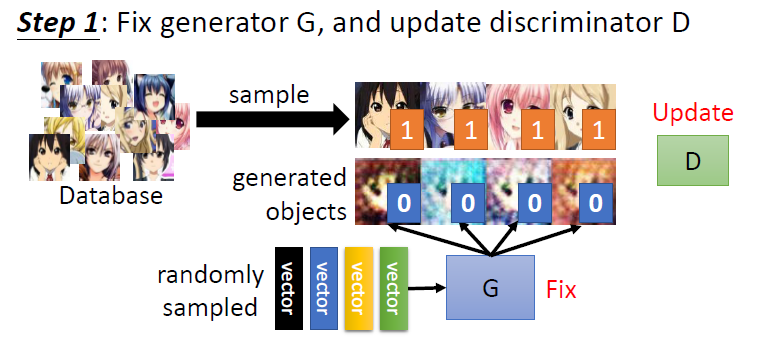
GAN的一轮训练基本流程如下:
- fix generator & update discriminator:
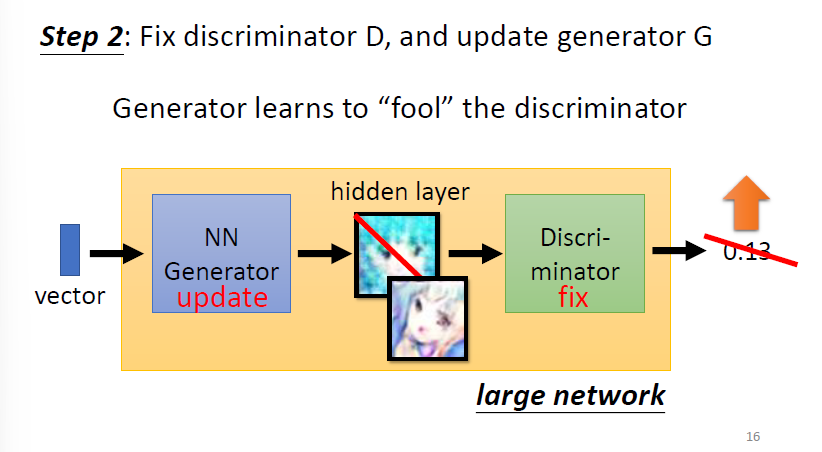
- fix discriminator & update generator:
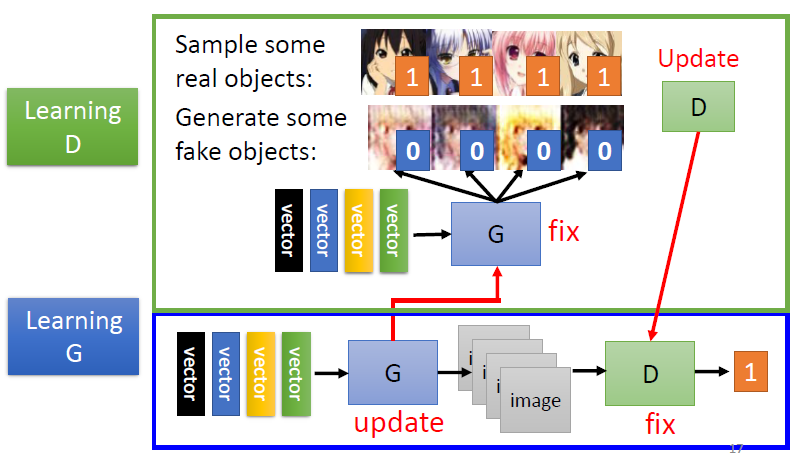
这样迭代若干轮,generator就可以获得不错的生成效果。
theory
GAN的优化目标是什么?考虑一个随机分布$x$,在经过generator $G$之后的分布为$P_G=G(x)$。而真实的data $data$经过generator $G$之后的分布为$P_{data}=G(data)$。我们的优化目标是$P_G=P_{data}$,或者: $$ G^* = \arg \min_G Div(P_G,P_{data}) $$ 由于$D$的本质是一个二分类训练器,我们定义损失函数$V(G,D)$(BCEloss): $$ V(G,D)=E_{y-P_{data}}[\log D(y)]+E_{y-P_G}[\log(1-D(y))] $$ 理想状况是,$D$倾向于将真实样本预测为正例,将生成样本预测为负例。这样我们要将$V(G,D)$最大化: $$ D^*=\arg \max_D V(D,G) $$ 两个优化阶段实际上是有联系的:当第一阶段的$Div$较小时,$D$较难分辨样本,反之则容易分辨样本。
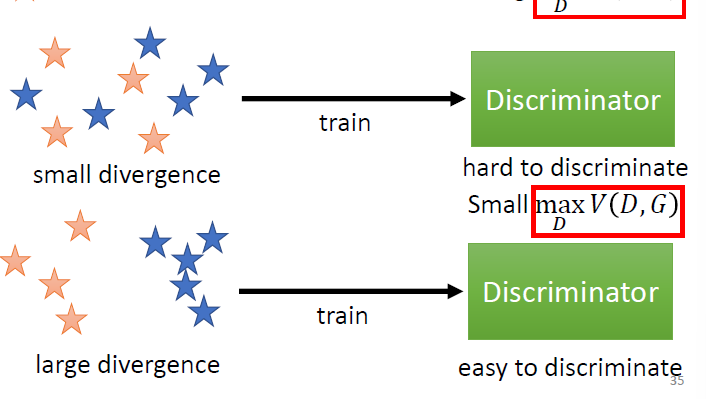
注意到$D$可以直接计算两种数据之间的$Div$。这样我们将$G$的优化函数改写如下: $$ G^*=\arg \min_G \max_D V(G,D) $$ 这个式子的含义是:生成器不断优化使得判别器准确率降低。
这里衡量GAN用到了散度的概念。传统深度学习(如知识蒸馏)多使用$\rm KL$散度: $$ KL(p||q) = -\int p(x)\ln \frac{q(x)}{p(x)}dx $$ 但$\rm KL$散度的一个缺点是不对称,于是我们定义$\rm JS$散度: $$ JS(p||q) = KL(p||\frac{p+q}{2}) + KL(q||\frac{p+q}{2}) $$
GAN以难以训练闻名。但其全局最优解是可知的,我们需要从数学上证明这两点:
-
对于任意给定的$G$,我们可以找到最优的判别器$D_G^∗$;
结论 $D_G^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_G(x)}$
-
对于全局最优的$G^∗$,我们希望它生成数据的分布和真实样本的分布一致,即$P_G=P_{data}$ 。
结论 当且仅当$p_G(x)=p_{data}(x)$时,我们才能得到$G$的全局最优解。
详细的证明见GAN详解
根据上述证明过程可以得出$G^=\arg \min_G \max_D V(G,D)$在最佳判别器$D_G^$的优化目标$C(G)=V(G,D_G^*)$可以写作: $$ C(G) = -\log(4)+2·JS(p_{data}(x)||p_{G}(x)) $$ 当$p_G(x)=p_{data}(x)$时,$C(G)$取得全局最优解$-\log4$。
other
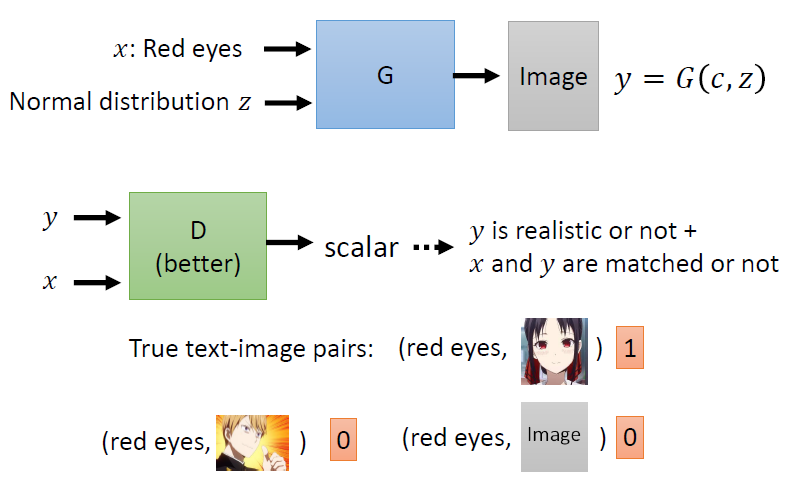
在基础版本的GAN中,模型输入的是随机分布。而当我们同时输入限定条件时,就得到了conditinal GAN。
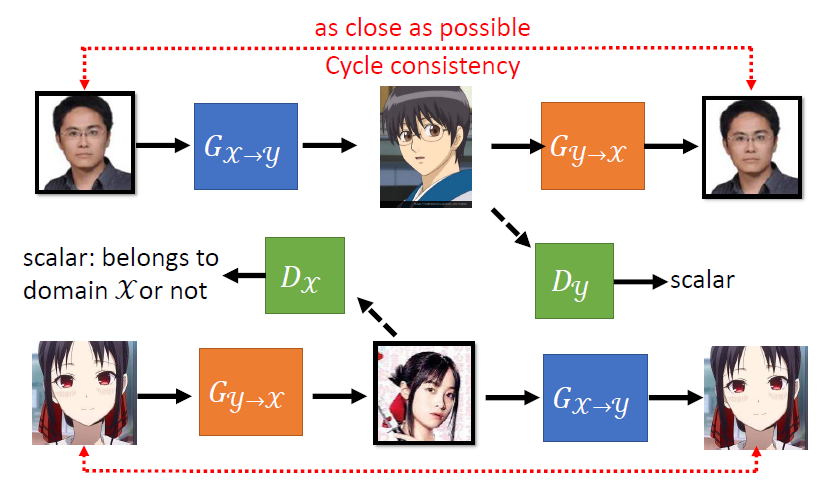
而使用不同风格的unpaired data,我们也可以实现风格迁移。比如我们需要实现$\mathcal{X}$ domain到$\mathcal{Y}$ domain的转换,generator $G_{x\rightarrow y}$负责风格转换,discriminator $D_{y}$负责判断真实的和虚假的$\mathcal{Y}$集。
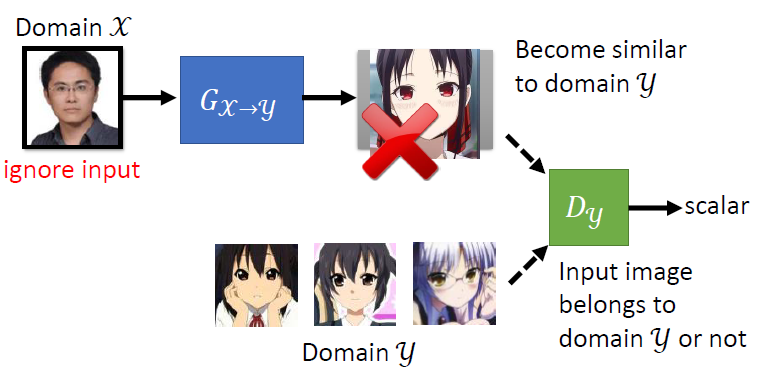
但这会导致一个问题:我们如何判断风格的迁移是否符合预期?为此,我们引入一个新的generator $G_{y\rightarrow x}$,判断生成的$\mathcal{X}$集是否与原本的$\mathcal{X}$集相似。为了进一步增强效果,我们还可以新引入一个$D_x$来增强效果,这就是Cycle GAN的效果: