前言
一直有自学CSAPP的想法,但如果专门报一门课去学的话,一方面和之前的部分培养方案有重叠,划不来;另一方面时间也真的不够充裕。反复思索之下,最终还是采用一种我愿称之为Lab Oriented Studying(LOS,面向实验学习)的方法简单过一遍。具体方法如下:先略读本章内容,然后在做lab的同时针对重点进行强化,同时大量借鉴别人的思路,力求在最短的时间内获得最大的收获。目前的计划是至少做(chao)完datalab、bomblab和attacklab,其他的lab可以先准备基础知识,顺便在OS课上巩固,然后在不(heng)远的将来完成,希望这个饼能实现(我本科已经留下这么多遗憾了,不会连这个小小的计划都把握不住吧x)。
bitXor
1
2
3
4
5
6
7
8
9
10
11
|
/*
* bitXor - x^y using only ~ and &
* Example: bitXor(4, 5) = 1
* Legal ops: ~ &
* Max ops: 14
* Rating: 1
*/
int bitXor(int x, int y)
{
return ~(~(x & ~y) & ~(~x & y));
}
|
since a|b = ~(~a & ~b), a & b = ~(~a | ~b) , so a ^ b = (a & ~b) | (~a & b) = ~(~(a & ~b) & ~(~a & b)).
and there is a simpler expression using fewer operators: ~(~x&~y)&~(x&y)
tmin
1
2
3
4
5
6
7
8
9
10
|
/*
* tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
*/
int tmin(void)
{
return 1 << 31;
}
|
31 bits 1 is the smallest representation in int32.
isTmax
1
2
3
4
5
6
7
8
9
10
11
|
/*
* isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
*/
int isTmax(int x)
{
return (!(~(x + (x + 1)))) & (!!(x + 1));
}
|
To see if x = 0b011111... = 0x7ffffff. 我们将该值记为x_{max},可以建立这样一个映射:该值会被映射为0/1,而其他值全部被映射为1/0,这样就可以使用简单的逻辑运算符判断。
首先我们看“如何把x_{max}转换为0”。为了得到“一个32个位上都为0”的数,我们执行以下操作:!~(x + (x + 1)),当x = x_{max}时显然为1。
之后我们再看“这一映射是否唯一”,上述表达这不能排除一种情况:x = 0xfffffff,对此我们还有一个判断:(x + 1) != 0,使用题中的符号表述就是!!(x + 1)。组合即得。
allOddBits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
/*
* allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
* Note: use value less than 256
*/
int allOddBits(int x)
{
int y = 0xAA + (0xAA<<8) + (0xAA<<16) + (0xAA<<24);
return !((x & y) ^ y);
}
|
判断所有的奇数位是否为1。该数应该和0b1010_1010_1010_1010与之后为0。注意x == y等价于!((x & y) ^ y。
negate
1
2
3
4
5
6
7
8
9
10
11
|
/*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
int negate(int x)
{
return ~x + 1;
}
|
常识,略。
isAsciiDigit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
/*
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
int isAsciiDigit(int x)
{
int max_val = ((~0x39) | (1 << 31));
int min_val = ~0x30;
return ((max_val + x) >> 31) & !((min_val + x) >> 31)
}
|
一开始的思路是逐个位地提取‘1’或‘0’,但不太可行,这样很容易就超出了运算符号数限制:
0x30的二进制形式为0b0011_0000,0x39的二进制形式为0b0011_1001。有以下特点:
- 4~7位一定为0011
- 0~3位中,在第3位为1的情况下第2和第1位一定为0
对此,可以构造两个数,使得:一个数是加上比0x39大的数后符号由正变负,另一个数是加上比0x30小的值时是负数。可见0x39与最大数相加后应该是0x7fffffff,0x30与最小数相加后应该是0xffffffff。
conditional
1
2
3
4
5
6
7
8
9
10
11
12
13
|
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
int conditional(int x, int y, int z)
{
x = !!x;
x = ~x+1;
return (x & y) | (~x & z);
}
|
我们可以把x这个“条件”转换成一种“掩码”,即一种情况下x为全0,另一种为全1,之后只要与运算一下即可。通过!!x这一运算得到布尔值,然后通过补码运算得到全1或全0。
isLessOrEqual
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
int isLessOrEqual(int x, int y)
{
int sign_x = (x >> 31) & 0x1;
int sign_y = (y >> 31) & 0x1;
int sub = y + (~x + 1);
int sign_int = (sub >> 31) & 0x1;
return (sign_x & ~sign_y) | (!(~sign_x & sign_y) & !sign_int);
}
|
首先根据negate我们可以用位运算实现减法y - x = y + (~x + 1)。之后需要提取出x和y的符号。此时我们需要考虑4种情况:
- x正y负:x大
- x负y正:y大
- xy同号:若大于,则符号位为0;若小于,则符号位为1
注意到这里不要用x - y,因为题目中要实现的符号是<=,因此运算结果中的正数和零应该都是等效的。
logicalNeg
1
2
3
4
5
6
7
8
9
10
11
12
|
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
int logicalNeg(int x)
{
return ((x | (~x + 1)) >> 31) + 1;
}
|
注意到0和0x80000000(最小数)的补码为本身。以及除了0之外,其他数与补码的符号位取位或为1。
howManyBits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
int howManyBits(int x)
{
int sign_x = (x >> 31);
x = (sign_x & ~x) | (~sign_x & x); // x >=0 ? x : ~x
int b16, b8, b4, b2, b1, b0;
int sum = 0;
b16 = !!(x >> 16) << 4; // 高十六位是否有1
sum = sum + b16;
x = x >> b16; // 如果有(至少需要16位),则将原数右移16位。注意我们直接将逻辑值移位得到真实需要的bit数
b8 = !!(x >> 8) << 3; // 剩余位高8位是否有1
sum = sum + b8;
x = x >> b8; // 如果有(至少需要16+8=24位),则右移8位
b4 = !!(x >> 4) << 2; // 同理
sum = sum + b4;
x = x >> b4;
b2 = !!(x >> 2) << 1;
sum = sum + b2;
x = x >> b2;
b1 = !!(x >> 1);
sum = sum + b1;
x = x >> b1;
b0 = x;
sum = sum + b0;
return sum + 1; //+1表示加上符号位
}
|
什么意思呢?写出这些数字的二进制表示:
1
2
3
4
5
6
|
12 -> 0b0000_0000_000(0_1100)
298 -> 0b0000_00(01_0010_1010)
-5 -> 0b1111_1111_1111_(1011)
0 -> 0b0000_0000_0000_000(0)
-1 -> 0b1111_1111_1111_111(1)
0x80000000 -> 0b(1000_0000_0000_0000)
|
如果是一个正数,则需要找到它最高的一位(假设是n)是1的,再加上符号位,结果为n+1;如果是一个负数,则需要知道其最高的一位是0的,再加上符号位。这一逻辑可以很容易地使用循环实现,不过此处无法使用for语句,只好使用一种类似“二分查找”的方法。
注意到正数和负数的判定特点,此处我们可以将负数直接取反变成正数,判断逻辑一模一样。
floatScale2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
/*
* floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatScale2(unsigned uf)
{
unsigned sign = (uf & 0x80000000) >> 31;
unsigned exp = (uf & 0x7f800000) >> 23;
unsigned frac = uf & 0x007fffff;
unsigned res;
if (exp == 0xFF)
return uf;
else if (exp == 0)
{
frac <<= 1;
res = (sign << 31) | (exp << 23) | frac;
}
else
{
exp++;
res = (sign << 31) | (exp << 23) | frac;
}
return res;
}
|
首先回忆下浮点数的构成:
$$
V = (-1)^s \times M \times 2^E
$$

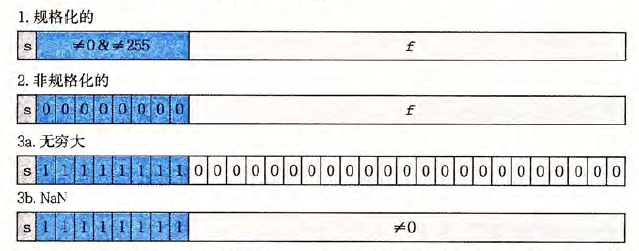
规格化时:
$$
E = e(e_{k-1}\cdots e_0) - bias \
M = 1 + f(f_{k-1}\cdots0) \
$$
非规格化时:
$$
E = 1 - bias \
M = f(f_{k-1}\cdots0)
$$
对于规格化的情况,我们只需:
$$
2V = (-1)^s \times M \times 2^{E+1}
$$
对于非规格化的情况,我们只需:
$$
2V = (-1)^s \times 2M \times 2^E \ (E = 0)
$$
此处考虑一种极端情况:非规格化数乘2之后变为规格化的数,此时M发生“溢出”,溢出的一位自动补在E的最后一位,E=1,根据其解释方法的变化,$2^E$的值实际上是没有变化的,但变换后的$M$等效于之前的$2M$,因此解释方法的变化有利于非规格化到规格化的转变。
无穷大和NaN直接返回即可。
floatFloat2Int
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
/*
* floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
int floatFloat2Int(unsigned uf)
{
unsigned sign = (uf & 0x80000000) >> 31;
unsigned exp = (uf & 0x7f800000) >> 23;
unsigned frac = uf & 0x007fffff;
unsigned E = exp - 127;
if (E >= 0xFF)
return 0x80000000u;
else if (E < 0)
return 0;
else
{
frac = frac | 0x00800000;
if (E > 23)
frac <<= (E - 23);
else
frac >>= (23 - E);
if (sign)
frac = ~frac + 1;
return frac;
}
}
|
首先考虑特殊情况:如果原浮点值为0则返回0;如果真实指数大于31(frac部分是大于等于1的,1«31位会覆盖符号位),返回规定的溢出值0x80000000u;如果 exp<0exp<0exp<0 (1右移x位,x>0,结果为0)则返回0。剩下的情况:首先把小数部分(23位)转化为整数(和23比较),然后判断是否溢出:如果和原符号相同则直接返回,否则如果结果为负(原来为正)则溢出返回越界指定值0x80000000u,否则原来为负,结果为正,则需要返回其补码(相反数)。
floatPower2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
/*
* floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatPower2(int x)
{
int exp = x + 127;
if (exp <= 0)
{
return 0;
}
else if (exp >= 0xFF)
{
return 0x7f800000;
}
else
{
return exp << 23;
}
}
|
题目的已知条件相当于告诉了指数位的代表大小,我们首先将其转换为浮点数指数位的形式,然后移位到指定位置,注意判定无穷大的情况。
注:c语言在执行右移时,执行的是算数右移还是逻辑右移?对于有符号数来说,执行算数右移;对于无符号数来说,执行逻辑右移。
1
2
3
4
5
6
7
8
9
|
#include <stdio.h>
int main()
{
int x = 0xffffffff;
unsigned int y = 0xffffffff;
printf("%d\n", x >> 31); // -1
printf("%d\n", y >> 31); // 1
}
|
Reference

